Система рейтингов Эло — метод расчета относительной силы игроков в играх, в которых участвуют двое. Разработчик системы — профессор физики Арпад Имре Эло (венг. Arpad Elo; 1903—1992).
На уровне низшего класса рейтинг Эло чаще дает неверные предсказания результата, так как эти игроки чаще совершают непредсказуемые ошибки.
Чем реже проигрывает игрок, тем точнее можно оценить его рейтинг. Наиболее точно рейтинг можно получить на основе турниров, в которых играют примерно равные по силам игроки.
В основе системы рейтингов Эло лежит допущение, что сила каждого игрока может быть представлена как вероятностная переменная, подчиняющаяся нормальному распределению. Расчет рейтинга игрока по результатам турнира основывается на сравнении количества набранных им очков с ожидаемым (на основе его текущего рейтинга). Рейтинг игрока возрастает, если по итогам турнира количество набранных очков оказывается больше, чем ожидаемое значение, и наоборот.
Вычисление рейтинга Эло
Новый рейтинг игрока рассчитывается по формуле:
Нов.Рейтинг = Преж.Рейтинг + K-фактор x (Факт.Результат-Ожид.Результат)
где:
K-фактор — коэффициент, значение которого равно 10 для сильнейших игроков (рейтинг 2400 и выше), 15 — для игроков с рейтингом меньше чем 2400 и 25 — для новых игроков;
Фактический результат рассчитывается путем сложения результатов партий турнира:1 очко за победу, 0,5 — за ничью и 0 — за поражение;
Ожидаемый результат игрока зависит от разницы между его рейтингом и средним рейтингом его соперников. Для облегчения расчетов ожидаемого результата профессор Эло составил специальную таблицу, в которой приводится ожидаемый процент набранных очков в зависимости от упомянутой разницы в рейтингах. Например, согласно этой таблице, если индивидуальный коэффициент шахматиста на 100 пунктов превышает средний рейтинг соперников, то он «должен» набрать 64% очков, если его рейтинг на столько же единиц ниже, то для сохранения его в неприкосновенности достаточно 36%.
Упрощенно таблица выглядит так: A- Разница рейтингов. В- Ожидаемый результат для игрока с более высоким рейтингом. С- Ожидаемый результат для игрока с более низким рейтингом
| А | В | С |
| 0 | 0,5 | 0,5 |
| 25 | 0,53 | 0,47 |
| 50 | 0,57 | 0,43 |
| 100 | 0,64 | 0,36 |
| 150 | 0,70 | 0,30 |
| 200 | 0,76 | 0,24 |
| 250 | 0,81 | 0,19 |
| 300 | 0,85 | 0,15 |
| 350 | 0,89 | 0,11 |
| 400 | 0,92 | 0,08 |
| 450 | 0,94 | 0,06 |
| 500 | 0,96 | 0,04 |
| 735 | 0,99 | 0,01 |
| >735 | 1,00 | 0,00 |
На сайте вычисление ожидаемого результата производится более точно, используя формулу:
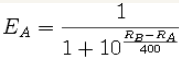
где EA: ожидаемое количество очков, которое наберёт игрок A в партии с B.
RA: рейтинг игрока A
RB: рейтинг игрока B
Так, если в турнире девять туров (наиболее распространенное число для массовых соревнований, проводимых по швейцарской системе), то ожидаемый результат соответственно равен 9*0,64=5,76 и 9*0,36=3,24. Обычно эти цифры округляются до ближайших 0,5 очка (5,5 и 3,5).
« Правила игры в Рэндзю и Гомоку Международная федерация рэндзю »
