The Elo rating system is a method for calculating the relative strength of players in games played by two. The developer of the system is Professor of Physics Arpad Imre Elo (Hungarian Arpad Elo; 1903-1992).

At the lower class level, the Elo rating is more likely to mispredict the outcome, as these players are more likely to make unpredictable mistakes.

The less often a player loses, the more accurately you can estimate his rating. The most accurate rating can be obtained on the basis of tournaments in which players of approximately equal strength play.

The Elo rating system is based on the assumption that the strength of each player can be represented as a probabilistic variable that follows a normal distribution. The calculation of a player’s rating based on the results of the tournament is based on a comparison of the number of points scored by him with the expected (based on his current rating). The player’s rating rises if, at the end of the tournament, the number of points scored is greater than the expected value, and vice versa.

Elo rating calculation

The new player rating is calculated by the formula:

New Rating = Previous Rating + K-Factor x (Actual Outcome-Expected Outcome)

Where:
K-factor – coefficient, the value of which is 10 for the strongest players (rating 2400 and above), 15 – for players with a rating less than 2400 and 25 – for new players;
The actual result is calculated by adding the results of the tournament games: 1 point for a win, 0.5 for a draw and 0 for a loss;
The expected result of a player depends on the difference between his rating and the average rating of his opponents. To facilitate the calculation of the expected result, Professor Elo has compiled a special table in which the expected percentage of points scored, depending on the mentioned difference in ratings, is given. For example, according to this table, if the individual coefficient of a chess player is 100 points higher than the average rating of his opponents, then he “should” score 64% of the points, if his rating is the same number of units lower, then 36% is enough to keep him intact.

Simplified table looks like this: A- Difference in ratings. B- Expected result for a player with a higher rating. C- Expected result for a player with a lower rating

A B C
0 0.5 0.5
25 0.53 0.47
50 0.57 0.43
100 0.64 0.36
150 0.70 0.30
200 0.76 0.24
250 0.81 0.19
300 0.85 0.15
350 0.89 0.11
400 0.92 0.08
450 0.94 0.06
500 0.96 0.04
735 0.99 0.01
>735 1.00 0.00
On the site, the calculation of the expected result is made more accurately using the formula:

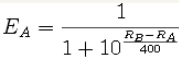
where EA: the expected number of points that player A will score in a game with B.
RA: player rating A
RB: player rating B

So, if there are nine rounds in the tournament (the most common number for mass competitions held according to the Swiss system), then the expected result is respectively 9*0.64=5.76 and 9*0.36=3.24. Usually these figures are rounded up to the nearest 0.5 points (5.5 and 3.5).